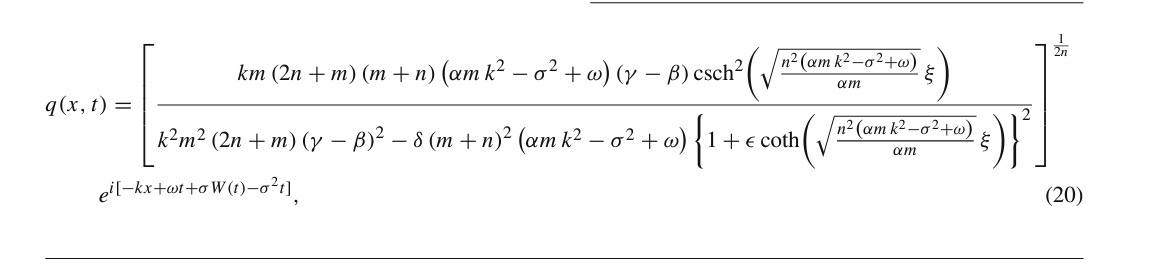I faced this problem before but i didn't remember how solve this issue for that parameter when i substitute and get solution How get two different solution also V(xi) must satisfy the odetest

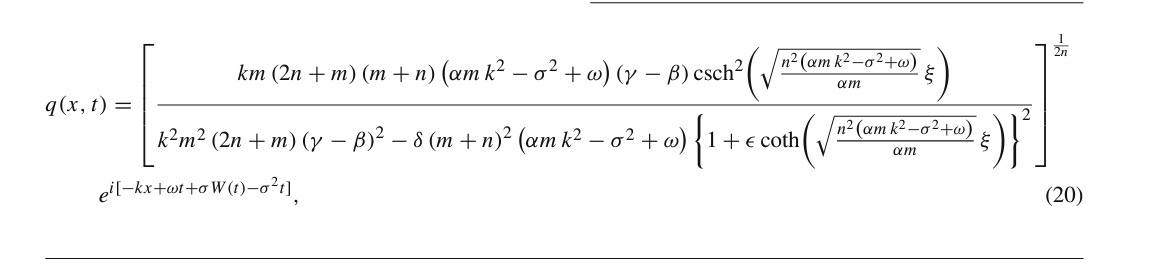

I faced this problem before but i didn't remember how solve this issue for that parameter when i substitute and get solution How get two different solution also V(xi) must satisfy the odetest